Basics for RFID
The following is excerpted from Chapter 3: Radio Basics for UHF RFID from the Book,
The RF in RFID: Passive UHF RFID in Practice by Daniel M. Dobkin.
Order a copy of The RF in RFID: Passive UHF RFID in Practice
before December 31, 2007 to receive an additional 20% off!
Visit www.newnespress.com or call 1-800-545-2522 and use code 91090.
While this book excerpt from The RF in RFID:Passive UHF RFID in Practice,
focuses on RFID applications, it is an excellent primer for RF basics.
Part 1 covers electromagnetic waves, signal voltage, and power.
Part 2 covers modulation and multiplexing.
Part 3 covers backscatter radio links and introduces link budgets.
Part 4 reveals how to determine the link budget.
Part 5 focuses on the effect of antenna gain on range.
Part 6 covers antenna polarization.
Part 7 covers antenna propagation.
Electromagnetic Waves
Recent estimates by cosmological folks suggest that around 95% of the mass in the universe is composed of dark matter and more recently minted dark energy, about which essentially nothing is known. Dark matter and dark energy don't appear to interact with our alternately glowing and dusty stuff except through gravitational means. Folks made of dark matter (if such were to exist) couldn't watch reruns of American Idol even if you forced them: they don't have any means of interacting with the broadcast signal and probably don't want to pay for cable.
For those condemned to the world of baryons and leptons, electromagnetic waves are a fact of life. In most textbooks on electromagnetic theory, you'll wade through Maxwell's equations and possibly laborious arguments on mysterious exchanges between the electric and magnetic fields launching self supporting structures with little Poynting vectors pointing out of them: all true but unnecessarily obscure. Before we go on to the mundane tasks of introducing the relevant terminology and technology of radio, let's share a little secret, implicit but not readily apparent in the standard texts, which the author has found to considerably simplify his view of electromagnetic radiation. It goes like this:
Everything radiates, but most things cancel.
To expand a bit: every object in the world that has an electric charge creates an electrostatic potential, which falls inversely as the distance. The potential sensed at some distance rcorresponds to what the charged object was doing at an earlier time (r/c), because signals move at the speed of light c = 3x108 m/s. The total electric potential in the space between your nose and the pages of the book you're reading depends on the amount of charge on the fur of a cat in Bulgaria (or Wisconsin, if you happen to be in Dobrich).
However, we almost never care, because electric charge comes in two flavors, positive and negative, and the amount of energy associated with an isolated charge of only one type is enormous: a microgram of hydrogen, split into its constituent protons and electrons and separated by 1 m, could support a mass of 8 million kilograms against the gravitational attraction of the entire earth. So in almost every case, adjacent to each electron with a negative charge is a proton with a positive charge, such that the two cancel, and have no net effect on your cellphone conversation. Electric currents similarly give rise to a magnetic vector potential in the direction of the current flow, which again exists everywhere with amplitude decreasing with distance, at a correspondingly delayed time.
Similar arguments show that most currents don't have any effect on distant objects. If a current is flowing in one direction, with no compensating countercurrent, charge must be accumulating somewhere, leading after a while to enormous energies (voltages). Most electric currents flow in a balanced loop: the potential from current flowing up cancels that from current flowing down, and again no net effect results on distant observers. These points are made pictorially in Figure 3.1, where we also introduce a bit of the mathematical terminology associated with the subject.
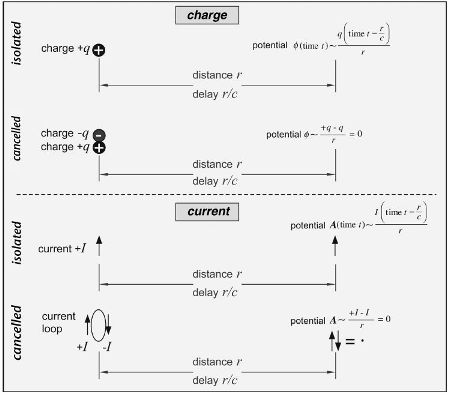
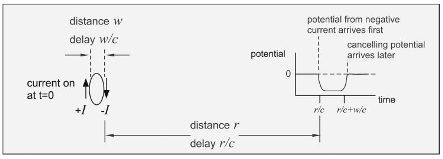
At first glance, we're left with no potentials and no waves, but, of course, this is not correct. For example, we can run an uncompensated current for a little while before charge accumulation causes too much voltage to build up and then turn it around. This uncompensated current will lead to a detectable signal at a distance. In addition, cancellation will often fail to be exact when the charges and currents are changing in time because of the slight differences in delays due to the finite size of the region over which the currents flow. For example, if in Figure 3.2, the loop current is suddenly turned on all around the loop at some time t = 0, the potential from the downward-flowing current arrives at r just a bit sooner than that from the upward-flowing current. Cancellation fails, and an observer sees some resulting potential:radiation has occurred.
This leads to our second key observation:
An antenna is a device to produce currents and charges whose effects don't cancel for a distant observer.
For an antenna to work, it should be apparent that something has to change: radiation is the result of the transient failure of delayed signals to cancel each other. In order to create a continuous signal, currents flowing on an antenna must continuously change, without actually getting anywhere: that is, currents and charges are usually periodic functions of time, alternately increasing and decreasing but returning to the same state again and again after the same interval. Periodic functions have a period—a time duration over which the signal is exactly repeated—and a frequency, conventionally measured in Hertz (Hz) and equal to (1/period). Thus, a signal that repeats itself every second has a frequency 1 Hz.
The sine and cosine are archetypal periodic functions, widely used in science and electrical engineering; in electrical engineering these are often combined into a complex exponential function, which absorbs both frequency and delay (phase) into one expression: eix = cos(x)+i sin(x), where i is the imaginary unit √(-1).
We should note that instead of arranging the currents on an antenna so as to frustrate cancellation at a distance, we can place the observer (the receiving antenna) so close to the transmitting antenna that cancellation is defeated simply because some currents on the transmitting antenna are close to the receiving antenna and have a larger effect than those more distant. This sort of interaction is known as near-field coupling or alternatively as inductive Coupling. We can think of inductive coupling as being fundamentally about differences in distance between differing parts of an antenna, whereas radiation is usually more closely related to differences in propagation time (phase) from one part of an antenna to another.
Armed with an antenna carrying a periodic current, we can create electromagnetic waves, propagating at the speed of light and falling in amplitude inversely with the distance (Figure 3.3).
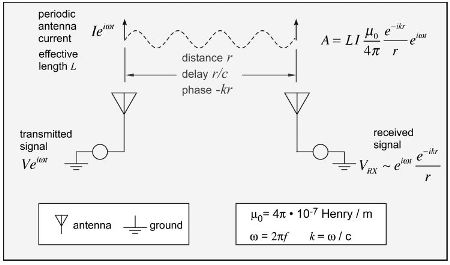
The waves induce a voltage in the receiving circuit, periodic with the same frequency as the transmitted signal, whose magnitude is inversely proportional to the distance between the transmitter and receiver. Using harmonic notation, the delay in time of Figure 3.1 becomes a phase offset by the wavenumber k multiplied by the distance r. (The absolute phase is often not readily observable or controllable in practical radio systems, so we can generally drop this term.) It is this voltage we make use of to transmit information—in the case of RFID, from a reader to a tag and back. How should we measure and describe it?
Describing Signal Voltage and Power
In most radio systems, we are interested in periodic currents and voltages since unchanging currents or voltages don't radiate as discussed above. Thus, a time-dependent signal voltage is usually written as the product of a magnitude (here v0) and a periodic function like the sine or cosine:

with an analogous expression for periodic currents. The instantaneous power dissipated into a load is the product of the voltage across the load and the current flowing through it. For a resistive load with a DC current flowing, we find:
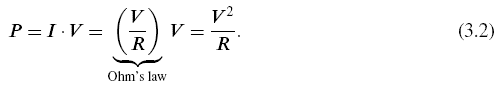
To get the average power for a periodic signal, we add up the total power over a cycle and divide by the cycle time. This gives us a factor of (1/2), the average value of cos2:

Sometimes people introduce the root-mean-square (RMS) voltage to eliminate the extra factor of (1/2) from the expression for power:
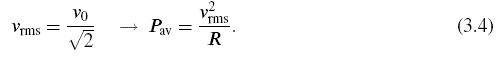
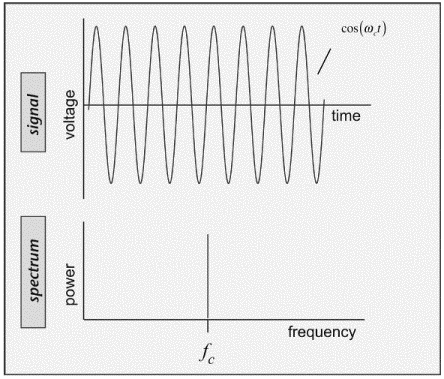
It isn't always obvious which definition of voltage is being used; confusion on this score leads to erroneous factors of 2 floating around. In this book, we will always use peak voltages and currents rather than RMS quantities, and thus, explicitly include the factor of (1/2) in calculating average power. It is often of interest to display the amount of power associated with a sinusoidal signal of a given frequency as apower spectrum; a simple example of such a display for the single-frequency signal of equation (3.1) is shown in Figure 3.4.
Signal power can vary over a huge range in typical radio practice: power dissipated into a typical 50-ohm load can range from tens of watts to 0.000 000 000 000 001 (10'15) watt. Related quantities, such as voltage, current, and gains and losses, span similar ranges. It is inconvenient to write out and manipulate such quantities as decimal numbers; instead, we use logarithmic notation. Recall that the base-10 logarithm is defined as:

For example, log(10) = 1, and log(1000) = 3. Negative logarithms denote numbers less than 1: log(0.001) = '3. It is traditional to use not raw logarithms, but deciBels (dB) in communications engineering. The ratio of two powers—for example, the ratio of the output power from an amplifier to the power that went in, which is the power gain of the amplifier—can be written in dB as:

Now, recall that the power is proportional to the square of the voltage. If we wanted to express the powers in equation (3.6) in terms of the corresponding voltages, we would get:
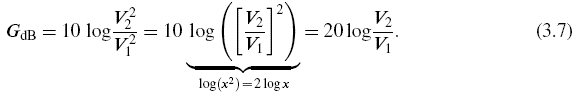
That is: dB are defined differently depending on the physical nature of the quantity being measured:
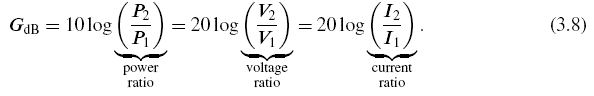
To define absolute power in dB, we need to decide on a reference level. In microwave engineering, the most common reference level is 1 milliwatt (mW), and power measured in dB relative to 1 mW is referred to as dBm:

Some practical examples of logarithmic notation are shown in Table 3.1 and Table 3.2. Because of the fact that log(ab) = log(a)+ log(b), dB add when the corresponding numbers multiply. A 1 microWatt signal that is passed through an amplifier with a power gain of 1000 produces 1 mW of output; we can equivalently say "-30 dBm +30 dB = 0 dBm."
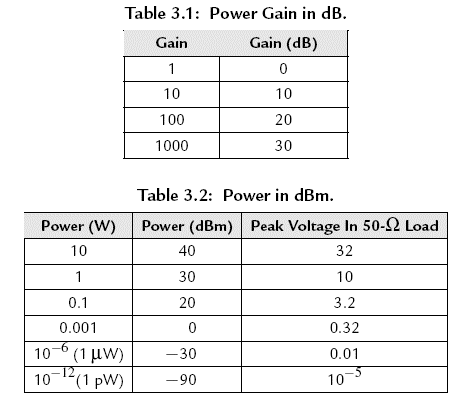
At the cost of memorizing a few quantities, one can almost obviate computation in converting from dB to numbers. A factor of 10 in power is 10 dB, and a factor of 2 is very nearly 3 dB. Since logarithms add, a factor of 4 = 6 dB, and a factor of 8 = 9 dB. Knowing these points allows quick, reasonably accurate estimates: for example, 50 μW = 1 mW/(10x2) = 0 dBm -10 dB -3 dB = -13 dBm.
Part 2 covers modulation and multiplexing.
About the Author
Dr. Dobkin has been involved in the development, manufacturing, and marketing of communications devices, components, and systems for 28 years. He holds a BS from the California Institute of Technology, and MS and PhD degrees from Stanford University, all in Applied Physics. He is the author of two books and about 30 technical publications, and holds 7 US patents as inventor or co-inventor. He has given numerous talks and classes on radio-frequency identification in the US and Asia. He specializes in physical-layer issues: radios and signal generation, antennas, and signal propagation. Dr. Dobkin lives in Sunnyvale, CA, with his wife, Nina, children Nicholas and Amelia, and entirely too many toys and video game consoles.
Copyright: Printed with permission from Newnes, a division of Elsevier. Copyright 2008. The RF in RFID: Passive UHF RFID in Practice by Daniel M. Dobkin. For more information about this title and other similar books, please visit www.newnespress.com
Information, Modulation, and Multiplexing
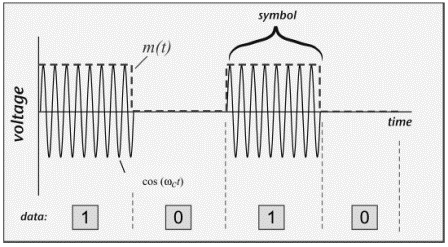
A periodic signal that persists indefinitely, without changing its amplitude, frequency, or phase—a continuous wave (CW) signal—carries no information other than the fact that it is present. In order to convey data, a signal needs to change. We normally think of this change as a relatively slowly changing variation—modulation—imposed on the periodic signal, for example:

The function m(t) is said to contain the baseband information, and the relatively high frequency cosine function is the carrier. When the function m(t) is another sine or cosine (presumably of much lower frequency), we can make use of trigonometric identities to rewrite the signal in a revealing fashion:
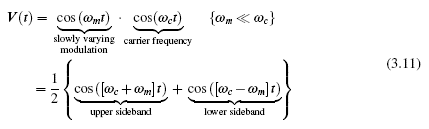
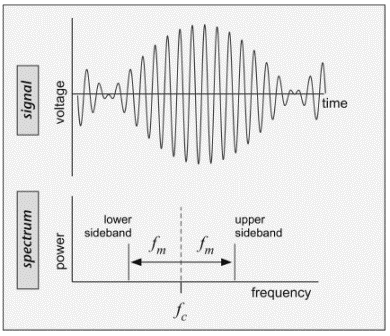
A sinusoidal modulation splits the carrier wave into two signals called sidebands, one above and one below the carrier, each displaced by the modulating frequency (Figure 3.5). While a continuous sinusoidal modulation is hardly more interesting or useful than a CW signal, this result suggests that when a signal is modulated, the resulting frequency spectrum becomes wider.
Signals of interest for RFID are generally digitally modulated. A digitally modulated signal is a stream of distinct symbols. A simple example with substantial relevance for RFID is on"off keying (OOK). The signal power is kept large (m = 1) to indicate a binary '1' and small or zero (m = 0) to represent a binary '0'. An example is shown in Figure 3.6. In OOK, each symbol is a period of fixed duration in which the signal power is either high or low.
Each OOK symbol represents one binary bit, though other types of symbols can convey more than one bit each. Any circuit that can change the output power, such as a simple switch, can be used to create an OOK signal, and any circuit that can detect power levels can demodulate (extract the data from) the signal. For example, a diode (an electrical component that passes electrical current only in one direction and blocks current flow in the opposite direction) can rectify a high-frequency signal, turning it into pulses of DC. These pulses can be smoothed with a storage capacitor to produce an output signal that looks very much like the baseband signal m(t). If the diode responds rapidly, it can be used at very high frequencies. Modern diodes can operate up to over 1 GHz, allowing passive RFID tags to demodulate a reader signal using only a diode and capacitor.
Unmodified OOK is admirably simple and seems promising as a method of modulating a reader signal. However, there is a problem with OOK for passive RFID. A passive RFID tag depends on power obtained from the reader to run its circuitry.
If that power is interrupted, the tag cannot operate. However, imagine the case of an OOK signal containing a long string of binary 0s: in this case, m = 0 for as long as the data remains 0. The tag will receive no power during this time. If the data remains '0' for too long, the tag will power off and need to be restarted, a situation not likely to be conducive to reliable operation. Even when some binary 1s are present, the power level delivered to the tag is strongly data dependent, an undesirable trait.
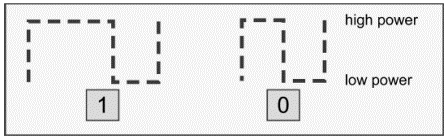
A common solution to the power problem is to code the binary data prior to modulation. One RFID coding approach is known as pulse-interval encoding (PIE). A binary '1' is coded as a short power-off pulse following a long full-power interval, and a binary '0' is coded as a shorter full-power interval with the same power-off pulse (Figure 3.7). The resulting coded baseband signal m(t) is then used to modulate the carrier (Figure 3.8).
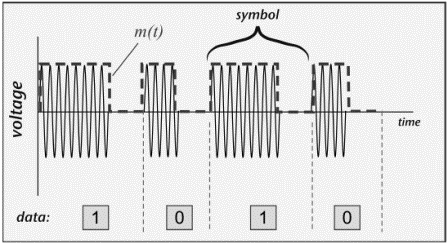
PIE using equal low and high pulses for a '0' ensures that at least 50% of the maximum power is delivered to the tag even when the data being transmitted contains long strings of zeros, and if the high is three times as long for a '1', a random stream of equally mixed binary data will provide about 63% of peak power. Note that in this case, the data rate becomes dependent on the data: a stream of binary 0s will be transmitted more rapidly than a stream of binary 1s. A single symbol has two features—the off-time and on-time—but still conveys only one binary bit. (This scheme is used in EPCglobal Class 1 Generation 2 readers. Other passive RFID standards use slightly different coding schemes, all generally characterized by the desire to have the reader power on as much as possible to power the tag.)
In fixing the problem with transmitted power by replacing OOK with PIE, we've made another problem worse. Radio waves travel everywhere, so in some sense the radio medium is shared between various users. For example, I would like to be able to read tags on packages in my storeroom despite the fact that the storeroom is also illuminated by the local broadcast radio and television stations, cellular phone basestations, the radio link from the taxi across the street, and the satellite downlink to the neighborhood cable TV system. Using a single medium for many signals is known as multiplexing. The most common form of multiplexing in radio, in use for almost a century, is frequency-division multiple access (FDMA): different users transmit using different carrier frequencies, and receivers are adapted to capture only the frequency of interest. (Signals can also be multiplexed in time and in coding. In RFID, time multiplexing is used when a reader uses an anticollision algorithm to poll tags one at a time.)
We will discuss the means used to filter the desired frequencies from the received signal in more detail in Chapter 4; for the present, it suffices to know that this operation can be accomplished. An RFID reader transmits on a frequency within the band at 902"928 MHz (in the United States), and listens to responses only within that band, rejecting the AM radio broadcast at 1 MHz, the television transmission at 52 MHz, the cellular transmission at 874 MHz, and so on.
This scheme would seem to allow an unlimited number of users to share the electromagnetic spectrum. However, recall that a signal must be modulated in order to convey information. When we modulate the signal, we increase the signal bandwidth. We saw an indication that this would be so in examining analog sinusoidal modulation of a signal (Figure 3.5). A modulated signal occupies a finite region of frequency, and neighbors must be separated by something like that amount in frequency to avoid interference.
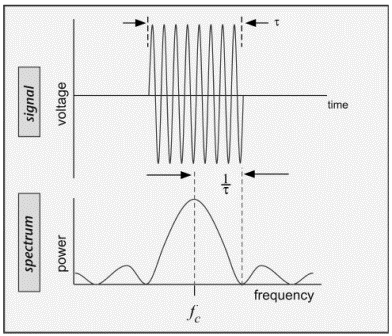
Furthermore, choices we make in modulation affect how much bandwidth we use. For example, if we modulate the signal faster by making the individual symbols take less time, that is, if we increase the data rate, we use more bandwidth. This phenomenon is illustrated in Figure 3.91, where we show the power spectrum of a modulated signal, and we have made use of the dB notation for spectral power introduced above.
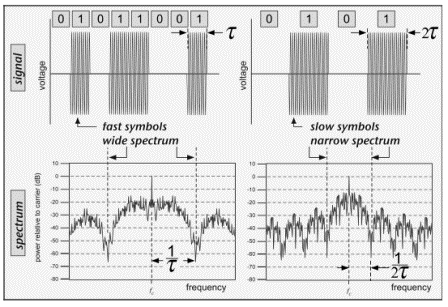
The spectrum has its largest power near the carrier frequency fc, but a considerable amount of power is transmitted at frequencies rather far from the carrier, as we might have suspected from Figure 3.5 above. The distance from the carrier frequency to the first major 'dip' in the spectrum is inversely proportional to the symbol time τ —that is, it is the same as the data rate R = 1/τ for OOK. The shorter the symbol time, the faster we can send data, but the more bandwidth we use. How we send symbols also matters. An abrupt step at the edge of each symbol gives more power far from the carrier than a smooth transition between low and high power states, as depicted in Figure 3.10. (Note that the residual power shown far from the carrier for the smooth symbols in this figure is affected by the specific method of smoothing the symbol and the accuracy of the numerical model.) Of course, the ability to smooth the transitions is limited by the duration of the symbols: at some point, changes happen so slowly that fully on or fully off states are never reached, causing the transmitted power to fall (and become data dependent).
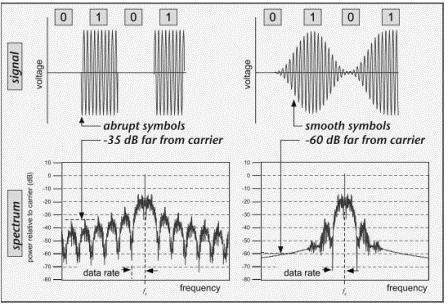
Smoothing the signals also makes the receiver's problem harder. It doesn't really matter when you test the voltage of a signal like that in left side of Figure 3.10 as long as you are within the symbol, but the smoothed signal on the right side is best sampled exactly at the center of the symbol, where the power is either at its maximum value or nearly zero. Sampling at any other times will result in more power for a nominal '0' or less power for a nominal '1': that is, the measured modulation depth is reduced. Thus, the receiver needs to do a better job of synchronizing with the incoming signal if that signal is smoothed.
Finally, the way we code the signal also matters. By examination of Figure 3.6 and Figure 3.8, we can see that pulse interval encoding will result in shorter pulses than OOK for the same data rate. So, from Figure 3.9, it seems likely that PIE would have a wider spectrum than OOK for the same data rate. This expectation is confirmed in Figure 3.11: substituting a stream of PIE symbols at the same average data rate for OOK symbols results in reduced power very near the carrier, but more power far from the carrier. In particular, a strong, narrow emission is seen at a frequency which turns out to correspond to (1/duration of a binary '0'); as depicted by the inset in the figure, the strong resemblance of a '0' symbol to a sine function results in a concentration of power at the corresponding frequency. The more diffuse band at half this offset results from the binary '1' symbol.
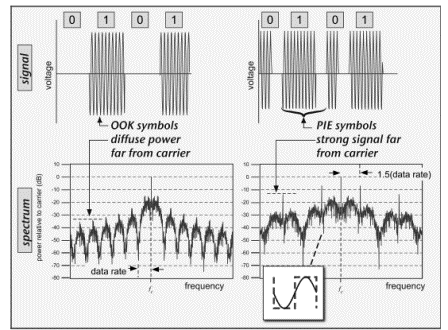
To clarify why this sort of thing matters in real applications, let's look at a practical example. In the United States, unlicensed readers randomly hop from one frequency to another within the ISM band from 902 to 928 MHz. Typically, RFID readers use channels that are 500 kHz wide and separated by 500 kHz. When a reader is trying to hear a tag, it transmits a signal of constant amplitude and phase. If reader #1on channel 10 is trying to hear a tag, while reader #2 on channel 11 is producing an emission spectra like those shown in Figure 3.11, the situation would look something like Figure 3.12, where the spectrum from reader #2 is scaled for a data rate of about 100 kbps and a distance of about 20 m. The leakage from reader #2 into reader #1s channel is thus comparable to or even larger than the tag signal; it will be difficult to detect the tag when reader #2 is transmitting data. Note, this is happening despite the fact that the tags are only 1 to 3 m from the reader, much closer than the interfering reader!
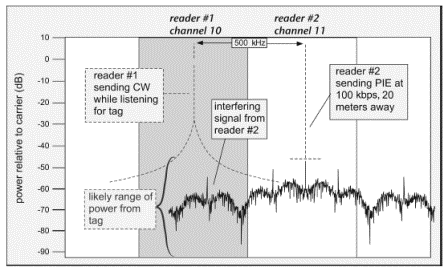
Even worse, if one of the readers happened to be near the edge of the ISM band, some of this power may be radiated outside of the allowed frequency range, potentially interfering with users of licensed frequencies, who have often paid for the privilege of exclusive use of said spectrum and get upset when they encounter freeloaders.
In the United States, the FCC requires that all radios be tested to ensure that such out-of-band radiation is minimized. Interference and out-of-band emissions represent important limits on how fast data can be transmitted by a reader, and on coding and modulation used, because the speed and method of modulation determine the bandwidth of the resulting signal. Let us pause for a bit of mathematics to clarify the frequency scales of the figures above. An ideal abrupt pulse (an OOK binary '1') of duration τ has a spectrum:

This function has some useful special values:
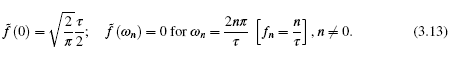
In particular, the first zero of this function is at a frequency of (1/τ), where τ is the duration of the pulse. When the signal is a modulated carrier wave, the spectrum is centered around the carrier frequency, and the zeros are displaced from the carrier by (1/τ) (Figure 3.13).
A stream of binary pulses (an OOK signal as in Figure 3.6) is just the sum of a number of these pulses, each with the same spectrum, so the full data stream will also have a spectrum with zero value at the same frequency offset from the carrier. These first zeros determine the width of the main lobe of the signal spectrum and are indicated by the dashed lines in Figure 3.9. Most of the power in the spectrum is contained within the region about half this wide, that is within a frequency range of (fc'1/(2τ)) to (fc +1/(2τ)). Thus, the narrowest channel that makes sense for an OOK signal is about twice as wide as the inverse of the data rate; we need 200 kHz to fit in 100 kbps.
PIE is much less efficient because the shortest pulse (the high part of a binary '0', Figure 3.8) is about 1/3 as long as an OOK pulse for the same data rate, so roughly three times as much spectrum is needed. To fit the main lobe of the spectrum within a 500 kHz channel, we can only use a data rate of around 85 kbps, which is just about the upper limit on reader data rates in United States operation, using unfiltered PIE-like modulations.
To summarize:
To convey information on a signal, the signal must be modulated.
Modulation causes the signal's spectrum to expand, requiring allocation of bandwidth in order to avoid interference.
The peculiar requirements of passive RFID lead to modulation and coding of binary data that are relatively inefficient in spectral use, limiting reader data rates.
It is important to note that more sophisticated radio systems, such as cellular telephony or IEEE 802.11 (WiFi), use modulation techniques that are substantially more efficient users of spectrum than PIE or OOK. However, these methods generally depend on the ability of the receiver to detect changes in the phase of the high-frequency signal rather than simply determining the power level, which passive RFID tags generally cannot do. Single sideband (SSB) and phase-reversal ASK (PR-ASK) modulations, which use phase information at the reader but require only amplitude detection from the tag, can be used to improve the spectral efficiency.
Backscatter Radio Links
Passive and semipassive RFID tags do not use a radio transmitter; instead, they use modulation of the reflected power from the tag antenna. Reflection of radio waves from an object has been a subject of active study since the development of radar began in the 1930s, and the use of backscattered radio for communications since Harry Stockman's work in 1949.
A very simple way to understand backscatter modulation is shown schematically in Figure 3.14: current flowing on a transmitting antenna leads to a voltage induced on a receiving antenna. If the antenna is connected to a load, which presents little impediment to current flow, it seems reasonable that a current will be induced on the receiving antenna.
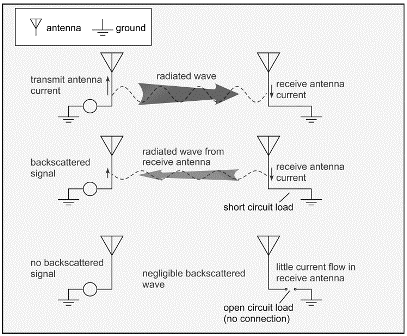
In the figure, the smallest possible load, a short circuit, is illustrated. This induced current is no different from the current on the transmitting antenna that started things out in the first place: it leads to radiation. (A principle of electromagnetic theory almost always valid in the ordinary world, the principle of reciprocity, says that any structure that receives a wave can also transmit a wave.) The radiated wave can make its way back to the transmitting antenna, induce a voltage, and therefore, produce a signal that can be detected: a backscattered signal. On the other hand, if instead a load that permits little current to flow (that is, a load with a large impedance) is placed between the antenna and ground, it seems reasonable that little or no induced current will result. In Figure 3.14, we show the largest possible load, an open circuit (no connection at all). Since it is currents on the antenna that lead to radiation, there will be no backscattered signal in this case. Therefore, the signal on the transmitting antenna is sensitive to the load connected to the receiving antenna.
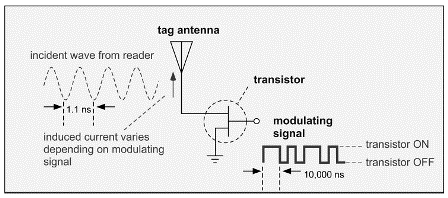
To construct a practical communications link using this scheme, we can attach a transistor as the antenna load (Figure 3.15). When the transistor gate contact is held at the appropriate potential to turn the transistor on, current travels readily through the channel, similar to a short circuit. When the gate is turned off, the channel becomes substantially nonconductive. Since the current induced on the antenna, and thus, the backscattered wave received at the reader, depend on the load presented to the antenna, this scheme creates a modulated backscattered wave at the reader.
Note that the modulating signal presented to the transistor is a baseband signal at a low frequency of a few hundred kHz at most, even though the reflected signal to the reader may be at 915 MHz. The use of the backscatter link means that the modulation switching circuitry in the tag only needs to operate at modest frequencies comparable to the data, not the carrier frequency, resulting in savings of cost and power. (Real RFID tag ICs are not quite this simple and may use a small change in capacitance to modulate the antenna current instead.)
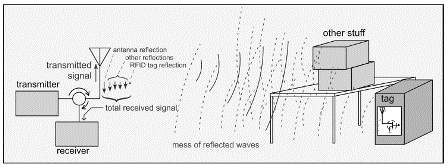
Note that in order to implement a backscattered scheme, the reader must transmit a signal. In many radio systems, the transmitter turns off when the receiver is trying to acquire a signal; this scheme is known as half-duplex to distinguish it from the case where the transmitter and receiver may operate simultaneously (known as a full-duplex radio).
In a passive RFID system, the transmitter does not turn itself off but instead, transmits CW during the time the receiver is listening for the tag signal. RFID radios use specialized components known as circulators or couplers to allow only reflected signals to get to the receiver, which might otherwise be saturated by the huge transmitted signal. However, in a single-antenna system, the transmitted signal from the reader bounces off its own antenna back into the receiver, and the transmitted wave from the antenna bounces off any nearby objects such as desks, tables, people, coffee cups, metal boxes, and all the other junk that real environments are filled with, in addition to the poor little tag antenna we're trying to see (Figure 3.16).
If two antennas are used (one for transmit and one for receive), there is still typically some signal power that leaks directly from one to the other, as well as the aforesaid spurious reflections from objects in the neighborhood. The total signal at the receiver is the vector sum of all these contributions, most of which are much larger than the wanted tag signal, with appropriate amplitudes and phases, most of which are unpredictable a priori. Thus, the actual effect of a given change in the load on the tag antenna on the receiver signal is completely unpredictable and uncontrollable. For example, modulating the size of the tag antenna current (amplitude modulation) may not result in the same kind of change in the reader signal.
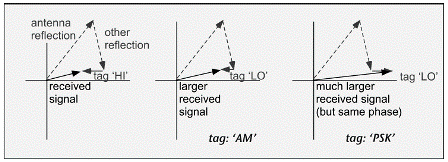
In Figure 3.17, we show a case where changing the tag reflection from a large amplitude (HI) to a small amplitude (LO) causes the received signal to increase in magnitude without changing phase (the "AM" case). Changing the phase of the tag signal without changing the size of the reflected signal in order to symbolize a local oscillator (LO) state may change the amplitude of the reader signal at constant phase (Figure 3.17, PSK case). The only thing we can say with any confidence is that when we make a change in the state of the tag antenna, something about the phase or amplitude of the reader signal will change.
In order to make a backscatter link work, we need to choose a way to code the data that can be interpreted based only on these changes and not on their direction or on whether they are changes in phase or amplitude. As a consequence, all approaches to coding the tag signal are based on counting the number of changes in tag state in a given time interval, or equivalently on changing the frequency of the tag's state changes.
Therefore, all tag codes are variations of frequency-shift keying (FSK). It is important to note that the frequency being referred to here is not the radio carrier frequency of (say) 900 MHz but the tag (baseband) frequency of perhaps 100 or 200 kHz. A binary '1' might be coded by having the tag flip its state 100 times per millisecond, and a binary '0' might have 50 flips per millisecond.
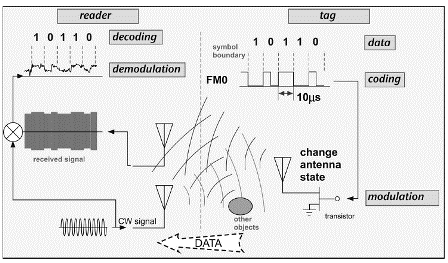
Because the frequency being changed is the frequency at which a carrier is being amplitude modulated, techniques like this are sometimes known as subcarrier modulation. Let's look at one specific example of tag coding, usually known as FM0 (Figure 3.18).

In FM0, the tag state changes at the beginning and end of every symbol. In addition, a binary 0 has an additional state change in the middle of the symbol. Note that, unlike OOK, the actual tag state does not reliably correspond to the binary bit: for example, in the left-hand side of the figure, two of the binary '1' symbols have the tag in the LO state and another '1' symbol has the tag in the HI state. Remember, the reader can't reliably distinguish which state is which but can only count transitions between them. The right side of the figure shows the baseband signal corresponding to a series of identical binary bits to clarify the correspondence of binary '0's with a frequency twice as high as that of binary '1's. Different tag coding schemes can be used to adjust the offset from the carrier frequency at which the signal from the tags is found. Readers have an easier time seeing a tag signal when it is well separated from their own carrier frequency, so higher subcarrier frequencies help improve the ability to read a tag signal. However, if the separation is large compared to the channel size, the tag signal might lie on the signal of another reader in a different channel. Just as with readers, increasing the data rate of a tag signal tends to spread the spectrum out in frequency. To have a flexible choice of tag data rates while minimizing noise, the reader needs to be able to adapt the band of frequencies it tries to receive, adding cost and complexity.
In real receivers, noise and interference may be present as well as the desired signal. A certain minimum signal-to-noise ratio (S/N) is necessary for each type of modulation in order that it can be reliably decoded by the receiver. The exact (S/N) threshold depends on how accurate you're trying to be and to a lesser extent on the algorithms used for demodulation/decoding. For RFID using FM0, (S/N) of around 10 or better (10 dB or more) is usually sufficient. (Requirements for demodulation of reader symbols, like PIE, in the tag are generally similar.)
Link Budgets
Let's summarize the message of the last couple of sections. To transmit to a tag, a reader uses amplitude modulation to send a series of digital symbols. The symbols are coded to ensure that sufficient power is always being transmitted regardless of the data contained within in. The received signal can be demodulated using a very simple power detection scheme to produce a baseband voltage, which is then decoded by the tag logic. The whole scheme is depicted in Figure 3.19.
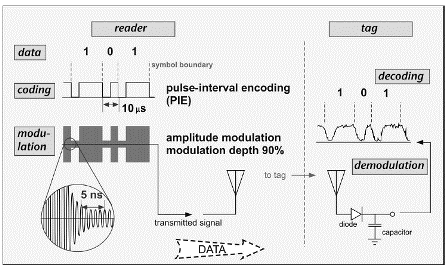
Figure 3.20 shows the corresponding tag-to-reader arrangements. The tag codes the data it wishes to send and then induces changes in the impedance state of the antenna. The reader CW signal bounces off the tag antenna (competing with other reflections) and is demodulated by the reader receiver and then decoded back into the transmitted data.
While we have alluded several times to the fact that the reader must power the tag, so far we have avoided coming to grips with the crucial associated question of just how much power the tag needs to get and just how far we can go from the reader and still get it. The amount of power that one needs to deliver to a receiver across a wireless link in order that the transmitted data be successfully received is known as the link budget. Since readers and tags both talk, for an RFID system there are two separate link budgets, one associated with the reader-to-tag communication (the forward link budget) and one with the tag reply to the reader (the reverse link budget).
In order to find the forward link budget, we need to know the following:
How much power can the reader transmit?
How much power does the tag receive as a function of distance from the reader?
How much power does the tag need to turn on?
How much power does the tag need to decode the reader signal?
Let's examine each question in turn.
Reader Transmit Power
The reader transmit power is set by a combination of practicality and regulation. Most RFID equipment operates in spectrum set aside for unlicensed use by the governmental body that regulates radio operation in a given jurisdiction. For example, in the United States, the FCC allows operation in the band 902"928 MHz without requiring that the person operating the equipment have a license to do so. However, the equipment itself must obey certain operating limitations in order to allow unlicensed use. Relevant for us at the moment is the maximum transmit power, which cannot exceed 1 W. While not all readers will deliver a watt, and in some applications, we may intentionally reduce transmitted power, in many cases a UHF reader will be operated at the legal limit. So let's assume we transmit 1 W of total power.
Path Loss
The difference between the power delivered to the transmitting antenna and that obtained from the receiving antenna is known as the path loss. In general, finding the path loss requires knowing something about the details of the antenna operation, and we shall discuss the relevant measurements and terminology shortly. However, to get started, we will use the simplest possible (not very accurate) approach: let us assume that the transmitting antenna radiates in all directions with the same power density, that is the transmitter is isotropic. We can picture the radiated power as being uniformly distributed over a spherical surface at any given distance r from the reader antenna (Figure 3.21). Some of this power can be collected by a tag antenna. It is reasonable to guess that the amount of power collected should be proportional to the density of power impinging on the tag and dimensionally necessary that the constant of proportionality be an area, often known as the effective aperture Ae of the tag antenna. Since in the isotropic case the power density at a distance r is the ratio of the transmitted power PTX to the sphere area, we can find the power received by the tag PRX:

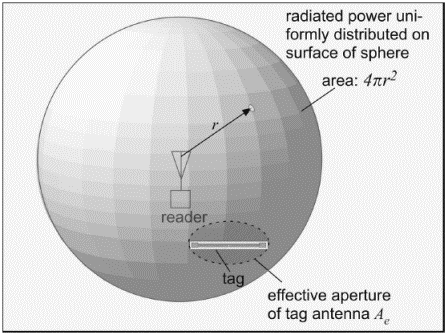
In order to get numbers out, we need a value for the effective aperture. It is not trivial to derive what this area should be, but it is plausible (and correct) to guess that the effective aperture of an antenna around a half-wavelength long might correspond to a square around a half wavelength on a side. The actual answer for an isotropic antenna (which a tag isn't quite) is:
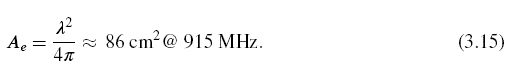
With a value for the aperture, we can now obtain an estimate of the path loss for our proposed isotropic link. At a distance of 1 m, the spherical surface has an area of 12.6 m2, so for 1 watt of transmit power, we get about 1(86)/(126,000) = 7 - 10'4 = 0.7 mW (-1.6 dBm). Since we started with a watt or 30 dBm, the path loss is about 32 dB.
Since the area scales with the square of the radius, we can very easily scale path loss, especially in dB: a factor of 10 in distance adds 20 dB to the path loss (20 dB/decade). A factor of 3 is worth just a bit less than half of this (about 9.5 dB). So at 3 m, the path loss is about (32+9.5) ≈ 41 dB, and at 10 m it is about 52 dB.
Tag Power Requirement
The tag antenna needs to deliver enough power to turn the tag IC on. We will consider this problem in some detail in Chapter 5; for the present, it suffices to give the results. Modern tag ICs actually consume around 10"30 μW to operate when being read (much more power is required to write new data to the tag memory). This power must be supplied by a rectifying circuit, which is about 30% efficient, due primarily to the substantial turn-on voltage required to make current flow through the diodes (see Chapter 5).
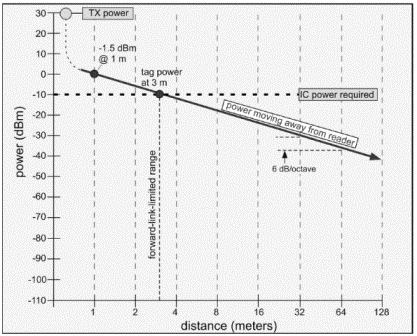
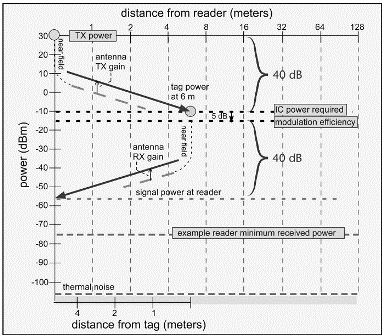
As a consequence, tags require about 30 to 100 μW of power to be delivered from the antenna to provide the required 10 to 30 μW of power to the chip. For simplicity, let us for the moment use a rather conservative 100 μW (-10 dBm) as the required threshold power. If we started at the transmitter with 1 watt (30 dBm), and we need to end up with -10 dBm, we have room for a path loss of (30-(-10)) = 40 dB. By reference to the previous paragraph, this corresponds to a distance of just less than 3 m. Thus, we expect the forward-link-limited range of a 1-watt reader connected to an isotropic antenna to be no more than about 3 m, for a tag that requires 100 μW to power up.
Most RFID readers use modulation depths (the extent to which the power is reduced in the low-power state of e.g., Figure 3.6 or Figure 3.8) of nearly 100%, so it is reasonable to guess that any time the tag has enough power to turn the IC on, it also receives more than enough signal power to interpret the data being sent by the reader.
The calculation is depicted graphically in Figure 3.22. We construct a line of slope -20 dB/decade (-6 dB/octave) and adjust the height of the line to give -1.5 dBm at 1 m. We can then immediately obtain the range as the intersection of this line with the required power for the IC, here taken as -10 dBm.
To perform the analogous calculation for the reverse link, we need to give thought to two additional issues:
How much power does the tag send?
How much power must the reader receive to demodulate and decode the tag data?
A passive tag does not generate its own carrier but simply modifies the amount of the incident radiation it backscatters. It is in principle possible for the tag to backscatter up to four times as much power as it could absorb; but, if it does so, the IC will receive no power at all. It is in principle possible to simultaneously deliver slightly less than the maximum absorbed power (e.g. -10 dBm in Figure 3.22) to the IC and scatter about the same amount of power back to the reader. In practice, this is challenging to accomplish.
Actual modulation efficiency varies from one design to another; a reasonable estimate for our purposes is to assume a modulated backscatter power around 1/3 of the absorbed power (that's -5 dB).
The amount of power the reader needs to receive is also complex and depends on a number of details of implementation we shall consider somewhat more thoroughly in Chapter 4. For the present purposes, we shall suggest a plausible and convenient lower limit of around -75 dBm (0.03 nW), deferring justification of this value until later. With the reader's indulgence, we shall proceed to use these unjustified assumptions to construct a diagram of the reverse link power in the same fashion as that previously constructed for the forward link; the result is depicted in Figure 3.23. We construct a second line like the first but starting at 5 dB less than the tag received power. Note that in this case, as the line descends, we are physically moving back towards the reader. If we move back 3 m (to intercept the dotted vertical line labeled 'forward-link-limited range'), we find the reader receives about -55 dBm, about 20 dB in excess of the power required by the reader's receiver. In fact, a receiver could be an additional 29 m away before the signal would fall so low as to fail to be received for this threshold value.
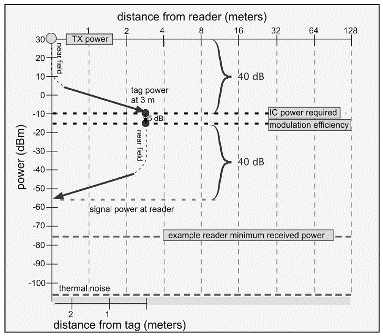
While the details of our simplified calculations are hardly authoritative, the observation that passive tags are forward-link-limited has historically been generally correct. The reason is that tag IC power requirements of tens or hundred of microwatts are actually monstrously large compared to the tiny signal powers that can be detected by a good-quality radio receiver.
However, as the required power delivered to the IC is decreased with continued progress in IC technology, this may change. To understand why, we need to understand how the power returned to the reader scales with tag-reader distance. Note in Figure 3.23 that the starting power for the tag scales with the received power.
If we double the distance to the tag, the power the tag receives falls by a factor of 4, and thus, the transmit power associated with the tag (the reverse link power) also falls by a factor of 4. But this power has to travel twice as far to get back to the reader, so the received power at the reader falls by an additional factor of 4. The net result for a doubling of the distance is a 16-fold (24) decrease in the received power at the reader. The received power from a backscatter link falls as the inverse fourth power of the distance:

In the case of a power-hungry passive tag, this scaling is rendered moot by the need to provide a fixed forward power to the tag. However, when the tag power is reduced by (say) 10 times, the forward-link-limited range increases by a factor of about 3. The received signal thus decreases by 20 dB, placing it at the threshold for this example receiver: the tag becomes reverse-link-limited (at least for this receiver). As we will see in Chapter 5, reader sensitivity is dependent on several design choices, particularly, antenna configuration, and will become more important as tag IC power is scaled to lower values. For a semi-passive tag, the forward-link requirement is much more lenient since the received power must only be decoded not exploited, and inverse-fourth-power scaling is very important in determining the range of the tag.
This part covers the effect of antenna gain on range.
We have been able to conclude that using an isotropic antenna, an RFID reader might achieve a read range of a few meters with 1 watt of output power. This configuration might be fine if RFID tags of interest are equally likely to be located in any direction with respect to the reader. However, such a circumstance is itself rather improbable. In the vast majority of cases, the reader antenna is placed at the edge of some region of interest, and the tags are to be located more or less centrally within this region, at some fairly well-defined angular relationship with the reader antenna. The power that is then being radiated in other directions is wasted (or worse, is reading tags outside the region of interest and confusing rather than enlightening the user). We could make better use of the transmitted power if we could cause the antenna to radiate preferentially along the directions in which tags are most likely to be found.
Fortunately, this is entirely possible to achieve. An antenna that performs this trick is known as a directional antenna. The operation of such an antenna is often depicted by showing an antenna radiation pattern; an example of such a pattern is depicted in Figure 3.24. For any direction d relative to the center of the antenna, the distance to the pattern surface represents the relative power density radiated by the antenna in that direction. The radiation pattern is an intuitively appealing method to represent the way a directional antenna concentrates its radiated power in a beam propagating in a particular direction.
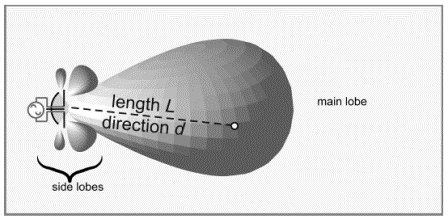
The ratio of the radiation intensity in any direction d to the intensity averaged over all directions is the directive gain of the antenna in that direction. The directive gain along the direction in which that quantity is maximized is known as the directivity of the antenna, and the directivity multiplied by the radiation efficiency is the power gain of the antenna (very often just referred to as the gain, G). In the direction of maximum radiated power density, we get G times more power than we would have obtained from an isotropic antenna of the type discussed in connection with Figures 3.21"3.23.
A note of caution is appropriate in considering the terminology we have just introduced. Antennas are passive devices and have no gain, in the sense that they can only radiate the power that is put into them, no more. The term antenna gain refers to the fact that, for a receiving antenna fortunate enough to be located along the direction of maximum power density, the received power is increased relative to that of an isotropic antenna just as if the output power of the directive antenna had been increased (isotropically) by a factor of G.
Of course, this has not actually happened; the radiated power has just been rearranged, and receiving antennas located in less fortunate directions receive much less power than would have been the case with an isotropic radiator.
The higher the gain of a directional antenna the more narrowly focused is the energy radiated from it. We can express the relationship mathematically by making the approximation that all the energy radiated by the antenna is uniformly distributed across a beam with some solid angle Ωbeam, and no energy is radiated elsewhere. In this case, the directivity of the antenna must be equal to the ratio of the beam solid angle to the total area of the unit sphere (4π), so we find that the solid angle is inversely proportional to the directivity (Figure 3.25). If the antenna radiates most of the energy it receives (which is usually the case for antennas with high directivity), the gain and directivity are about the same, so the size of the beam is inversely proportional to the gain. The beam angle is roughly the square root of the beam solid angle when the beam is reasonably symmetric.
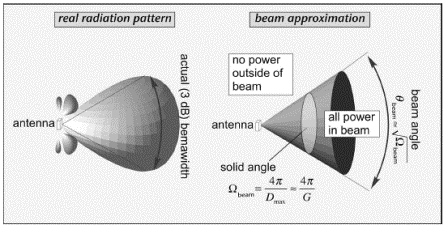
Pseudo-3D depictions of the radiation pattern are helpful to visualize complex geometries, but are difficult to obtain quantitative information from when printed. It is traditional to extract slices of the true radiation pattern in planes that pass through symmetry axes of the antenna.
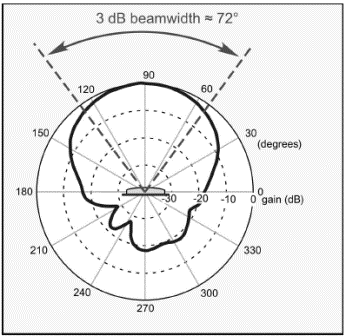
These may be labeled as altitude and azimuth, or sometimes E-plane and H-plane patterns (the notation refers to the planes in which the electric and magnetic fields are located and needn't concern us here). An example of such a pattern diagram for a real commercial directional antenna usable for RFID readers is shown in Figure 3.26.
This particular antenna used is known as a panel or patch antenna because it is constructed of a metal patch suspended over a metal ground plane, though the user cannot see these details unless they have the courage to slice up the nice-looking plastic casing. This particular pattern is plotted on a logarithmic radial scale, but linear scales are also used. By simply finding the locations at which the gain is reduced by 3 dB from the maximum value in the center of the beam, we can extract the 3 dB beamwidth, as has been done in this figure. Since 72° ≈ 1.25 radians, we can estimate the beam solid angle to be about (1.25)2 = 1.6 steradians, so the antenna gain must be roughly G ≈ 4π/1.6 ≈ 8, or 9 dB. (The actual gain of this antenna as reported on the data sheet is about 8.5 dB, so our simple calculation has produced a quite acceptably accurate result. However, the gain is also influenced by the power in the sidelobes and deviations of a couple of dB from this simple formula are not uncommon.) Practical, usable commercial antennas can provide us with quite substantial gains relative to an isotropic antenna.
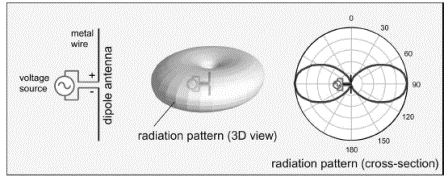
Not all antennas are highly directional. Though it turns out to be impossible to fabricate a truly isotropic antenna, one can come fairly close to this ideal. A very common example of a not-very-directional antenna is the dipole antenna (Figure 3.27). A dipole is constructed of two pieces of collinear wire driven by opposed voltages. Many RFID tag antennas are variants of a simple dipole. Dipole antennas do not radiate along their axes but radiate equally well in every direction perpendicular to the axis. Thus, the radiation pattern looks rather like a donut (or a bagel, depending on your nutritional inclinations). The gain of a typical dipole roughly half a wavelength long (16 cm at 900 MHz) is about 2.2 dB.
The gains we have been quoting so far are all measured with respect to an ideal (nonexistent) isotropic antenna and are often written as dBi to denote that reference state. In practice, gain is measured by comparing the received power of an antenna under test to a reference antenna, the latter often being a standard dipole antenna. Thus, it is easy to measure and report the gain of an antenna relative to a dipole, and this is sometimes done; such gains are usually written as "dBd." Since a dipole has 2.2 dBi of gain, gain referenced to a dipole is 2.2 dB less than gain referenced to an isotropic antenna: dBd = dBi -2.2.
Given the gain and transmit power of an antenna, we can calculate how much power we would need to put into an isotropic antenna to get the same peak power as we get in the main beam of a directional antenna (Figure 3.28). This power is called the effective isotropic radiated power (EIRP). The EIRP is larger than the actual power by the antenna gain, or in dBm:
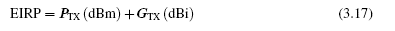
EIRP is often either explicitly or implicitly used as a regulatory limitation on radio operations because it is the EIRP rather than the transmitted power, which determines the peak power density transmitted by a reader, and thus, the likelihood that it will interfere with other users of the same frequency bands. For example, FCC regulations in the United States allow an unlicensed transmitter to use up to 1 watt of power with an antenna with 6 dBi of gain; for each dB of additional antenna gain, the transmit power must be reduced by 1 dB. In effect, the FCC is requiring that the EIRP not exceed +36 dBm (30 dBm + 6 dBi).
A closely related quantity, the effective radiated power (ERP) is also used in similar contexts. However, this term is used rather more loosely: web references can be found in which it is defined in an identical fashion to EIRP, though the United States FCC defines ERP as being referenced to a half-wave dipole antenna. In this book, we will define ERP following the FCC definition:
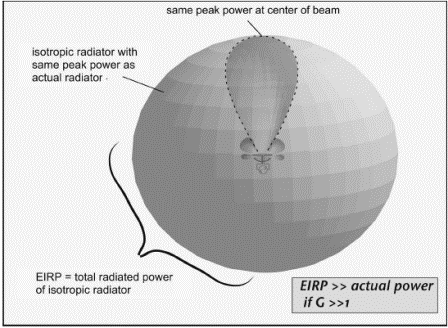
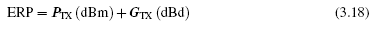
where as the reader will recall, gain in dBd is defined relative to a standard dipole antenna rather than relative to an isotropic antenna. However, we shall generally encourage the use of EIRP rather than ERP since the former is unambiguously defined.
Recall that the purpose of this digression into antenna behavior was to see if we could improve the performance of our theoretical RFID reader by using a directional antenna. If we use a directional antenna to transmit the 1 watt of allowed power and the RFID tag of interest is located within the main beam of that antenna, we would expect the transmitted power density to be increased by the gain of the antenna. The result ought to be an increase in the read range. The argument is depicted graphically in Figure 3.29, for an antenna with 6 dBi of gain.
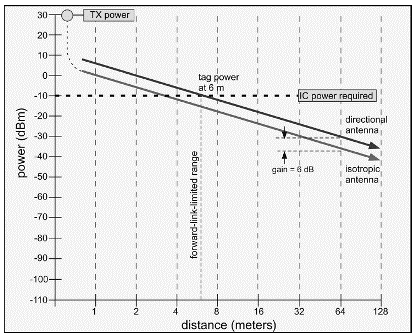
The forward-link-limited range has doubled, from 3 to 6 m, relative to that obtained in Figure 3.22. This is what we'd expect: we increased the signal power by a factor of 4, but power falls as the square of the distance, so this only provides us with a factor of 2 in range. At the same time, we've reduced our ability to see tags outside the main beam, presumably around 80 to100° wide here, which is usually desirable: by using a directional antenna we are able to (mostly) select the region in which tags can be read, and thus exclude tags that are not of interest.
What about the reverse link? In considering the action of an antenna as a receiver, we have heretofore asserted without detailed proof that the antenna collects energy from some effective aperture, and given a typical size. In fact, the size of the receiving aperture of any antenna is directly proportional to the gain of the antenna when used as a transmitter. This is a consequence of the principle of reciprocity, briefly alluded to previously, which for our purposes, we can state as: transmitting from antenna 1 and receiving with antenna 2 ought to give the same result as transmitting from antenna 2 and receiving with antenna 1. Since we have already cited the effective aperture for an isotropic antenna (equation (3.15)), we can write:

where the gain G is measured relative to an isotropic antenna, that is in dBi. Using this relationship, we can write a very general equation for the power received from a transmitting antenna TX by a receiving antenna RX if both gains and the distance between them are known:
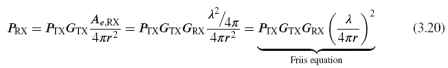
The last form of the relationship is known as the Friis equation, a very convenient way to state the expected received power. Note that this equation does not imply, as is sometimes erroneously asserted, that waves fail to propagate as wavelength decreases; from the derivation it should be apparent that the factor of λ2 arises from the effective aperture of the receiving antenna and is not related at all to propagation in the intervening space.
With the Friis equation in hand, we can immediately draw the reverse-link diagram for a directional antenna: the received power is simply increased by the antenna gain, just as the transmit power was. The result is given graphically in Figure 3.30. The received power is the same as in the isotropic case, even though the tag is twice as far away because the power at the tag is the same in both cases, and the received power is decreased by 6 dB due to the larger distance but increased by 6 dB due to the receiver antenna gain.
We can also construct a mathematical statement of the same relationships using the Friis equation. We define the gain of the tag antenna Gtag and a backscatter transmission loss Tb (= 1/3 or '5 dB here). We then have:
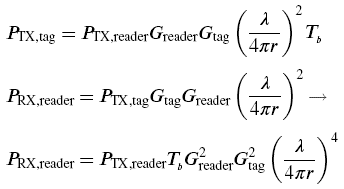
As promised, in the most general case, the power received at the reader goes as the inverse fourth power of the (symmetric) distance. It is also proportional to the square of the antenna gains, so when reverse link power is important (e.g. when a semipassive tag, or an unpowered device like a surface-acoustic-wave (SAW) tag, is used) the antenna gain plays a very large role in achievable read range. We have previously treated the tag antennas as having a gain of 1 (0 dBi). Real tag antennas have some gain, but it is typically modest (around 2 dBi, since they are usually dipole-like), and since we don't always control the exact orientation of the tag antenna and may not be able to guarantee that the main beam of the tag antenna is pointed at the reader, it is prudent to count on minimal gain from the tag antenna.
This part covers antenna polarization.
Real tag antennas have some gain, but it is typically modest (around 2 dBi, since they are usually dipole-like), and since we don't always control the exact orientation of the tag antenna and may not be able to guarantee that the main beam of the tag antenna is pointed at the reader, it is prudent to count on minimal gain from the tag antenna.
Using the Friis equation, we can also, after a bit of algebra, provide a couple of convenient range equations that can be useful for quick estimates. First, defining the minimum power, the tag requires as Pmin,tagwe obtain the forward-link-limited range:

and defining the minimum signal power for demodulation at the reader as Pmin,rdr, we obtain the reverse-link-limited range:

One additional antenna parameter is of vital importance in RFID. The radiated magnetic vector potential occurs in the direction of the current from which it radiates. The vector potential has a direction at each point in space. The electric field, which is derived from the vector and scalar potentials, describes the effect these potentials have on electrons in a wire. It is always pointed along that part of the vector potential that is perpendicular to the direction of propagation.
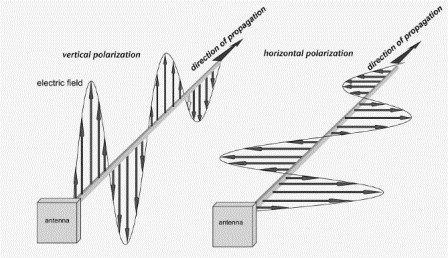
This isn't as scary as it sounds: it just means that electromagnetic waves are normally transverse waves. Like a wave on water, the effect associated with the wave is perpendicular to the direction in which the wave is propagating. When the wave from a boat strikes a buoy, the buoy (mostly) moves up and down, and only slightly towards or away from the passing boat. An electromagnetic wave moves electrons in the plane perpendicular to the direction of propagation, not along the direction of propagation. The direction in which the field points determines the polarization of the radiated wave. When this direction is constant in time, the wave is said to be linearly polarized.
Unlike water waves, electromagnetic waves are not influenced by gravity, and the electric field can point in any direction in the plane perpendicular to the direction of propagation. Because human beings are gravitationally challenged, it is most common to orient linearly polarized antennas either vertically or horizontally (Figure 3.31). However, any intermediate angle is also possible.
It is also possible for the direction of polarization to be time dependent. For example, the electric field can rotate around the axis of propagation as a function of time, without changing its magnitude, producing circularly polarized radiation (Figure 3.32).
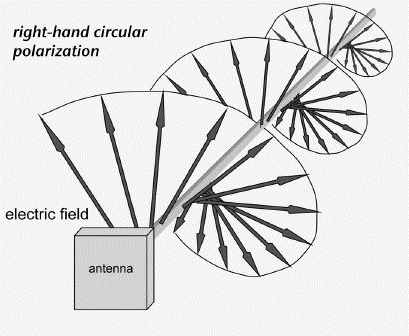
Depending on the sense of rotation, we obtain either right-handed or left-handed polarization. Note that the electric field of a circularly polarized wave still points in a specific direction at each moment in time, or at each location along the wave. Circular polarization does not refer to circulating fields or potentials but merely to the time dependent orientation of the field.
Circularly polarized radiation can be regarded as the sum of vertical and horizontal polarized waves that are out of phase by 90deg. By adjusting the ratio of horizontal and vertical components, and their phase relationship, we can produce elliptically polarized waves of arbitrary orientation, extending from pure circular to pure linear polarization.
The importance of polarization in RFID is simple to grasp: many RFID tag antennas consist primarily of narrow wire-like metal lines in one direction. If the electric field is directed along the wire, it can act to push electrons back and forth from one end of the wire to the other, inducing a voltage that is used to power the IC and allow the tag to reply. If the electric field is directed perpendicular to the wire axis, it merely moves electrons back and forth across the diameter of the wire, producing negligible current, no detectable voltage at the IC, and thus no power.
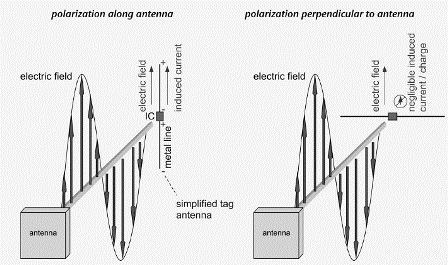
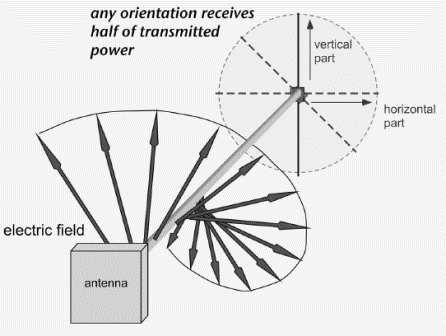
When a circularly polarized wave impinges on a linear antenna, only the component of the wave along the antenna axis has any effect. Thus, a circularly polarized wave will interact with a linear antenna tilted at any angle within the plane perpendicular to the axis of propagation, but in every case only half the transmitted power can be received.
A modest improvement in this situation results when physically larger 'bow-tie'-like antenna designs are used since electric fields at small angles to the axis of the antenna can still induce current flow. The best approach to fabricating tags that are polarization independent is to incorporate two dipole antennas on the tag directed orthogonally to one another; such tags are known as dual dipole designs. Note that it is necessary to separately rectify the power from each antenna in order to obtain polarization independence; if we simply add the signals from the two antennas and rectify the result, all we have accomplished is to create a new preferred orientation for linearly polarized waves.
In calculating the link budget, we can take into account polarization for simple linear antennas by projecting the incident electric field onto the polarization axis of the antenna. For the case of linear polarization, we just need to multiply by the cosine of the angle between the transmitted polarization and the receiving antenna axis, θpol, to get the effect of polarization on the induced voltage. The Friis equation becomes:
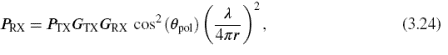
and thus the forward-link-limited read range will be found to be proportional to the cosine of the misalignment angle.
Note, finally, that because electromagnetic waves are transverse, there is no electric field along the direction of propagation. A simple linear tag antenna oriented along the direction of propagation (that is, pointing towards the reader antenna) sees no electric field along the wire axis and therefore receives no power.
The polarization of a simple wire antenna is easy to establish by inspection. The polarization of a commercial antenna, particularly when encased in a plastic radome, is not so obvious, and the user must usually refer to the labeling on the antenna or the manufacturer's data sheets, or use a linearly polarized tag to test the polarization of the radiated field. Antennas more complex than simple dipoles may not have the same polarization in all directions; circular polarization often becomes elliptical as the direction of observation moves away from the axis of the main beam.
Propagation in the Real World
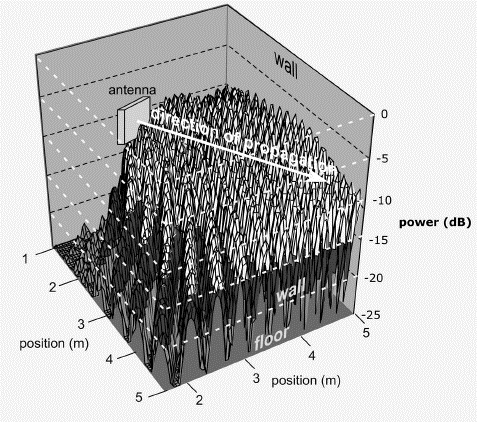
All the calculations we've performed so far assume that a wave leaves the antenna and strikes the tag, interacting with no other objects. This kind of calculation is very sensible if the tag and reader are placed in a specially designed anechoic chamber, or perhaps suspended high in the air from (nonmetallized) balloons. In the actual circumstances in which most readers and tags are used, the wave emitted from a reader antenna is likely to interact with many other objects besides the tag.
The interaction between waves that travel along the direct path between the reader and the tag, and those that are scattered or reflected, is of counter-intuitively large importance because it is voltages not powers that add. Let us consider, for example, the addition of a direct beam and two reflected beams, perhaps from the floor and a distant wall (Figure 3.35), each of which contains only 1/10 of the power of the direct signal. We can write the resulting voltage as:
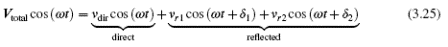
Here the δs are the phase differences between the reflected waves and the direct wave. The phase difference depends on the relative length of the path traveled by each wave; a change in that path of 8 cm (a quarter of a wave) corresponds to a 90-degree phase shift (from a maximum value to zero or vice versa) for the beam traveling that path. It is unlikely (!) that we can measure or control the position of every object in the room to within a couple of centimeters, so we must consider these phase delays as being generally unpredictable and uncontrollable.
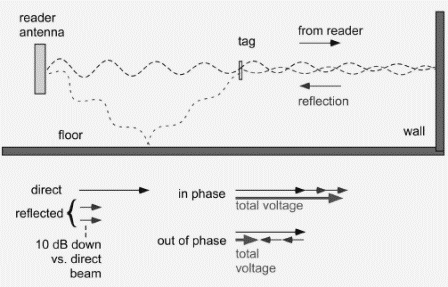
Thus, the best we can do is to examine the extreme cases. First of all, what if the reflected beams happen to both be in phase with the direct beam (δ = 0°)? We get:
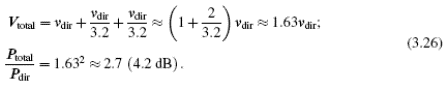
The received power is about 4 dB higher than in the absence of reflections. On the other hand, if the reflected beams are exactly out of phase (that is, δ = 180 deg;), we find:
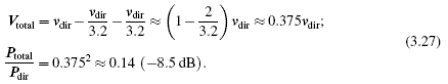
We have so far considered only unimpeded straight-line propagation, and specular reflection (where the angle of incidence and the angle of reflection are the same). In UHF RFID, the typical wavelengths of around 32 cm are comparable to the size of many obstacles present in the environment, so to fully treat the propagation environment, we must account not only for propagation and reflection, but diffraction: the ability of obstacles of finite size to scatter the incident radiation in directions other than specular. The full treatment of diffraction is rather complex, and not as important for passive RFID as for other communications fields since the forward link budget is so small.
The importance of diffraction may be roughly estimated by calculating the effective size of an obstacle in terms of the phase difference between the shortest and longest paths through the obstacle (Figure 3.39). In the figure, the shortest distance is the direct path (which passes right through the obstacle) and the longest distance goes around the edge of the obstacle. The phase difference is the difference in these path lengths multiplied by the wavenumber k = ω / c:

(A typical value of k for UHF RFID is about 19-20 radians/m.) This difference, measured in half-wavelengths (i.e. δ φ/ π, since there are 2π radians of phase in one wavelength), is the number of Fresnel zones subtended by the object. When this number is small (on the order of 1-2 or less), diffraction is important, and the received intensity is a complex function of position, with no well-defined shadow region. When the obstacle subtends many Fresnel zones (>3-5), it is able to form a fairly well-defined shadow, and tags in that region are unlikely to be visible to the reader.
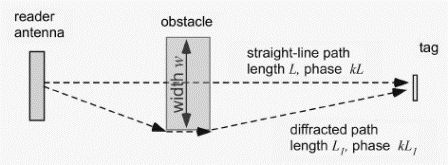
Consider, for example, a disk of diameter 1 m, illuminated by a reader antenna 2 m from the disk. If a tag is placed 5 cm behind the disk, the difference between the direct path and the path that goes around the edge of the disk is about (2.56"2.05)=0.51 m, which is about 3 Fresnel zones at 915 MHz (0.51/0.16). The tag is likely to find itself in a deep shadow and not be read (though it is worth noting that if the tag is carefully positioned exactly along the axis of the disk, it will find itself in a relatively high-intensity region in the middle of the shadow, known as Poisson's bright spot, which may allow it to power up). On the other hand, if the tag is placed 2 m from the disk, the path length difference becomes 0.12 m, rather less than one Fresnel zone, corresponding to weak and complex shadowing.
In this position, the tag will move in and out of faded regions as its position relative to the disk and reader changes. In practice, such weak shadowing often simply adds to the complex fading behavior resulting from walls, floors, and other obstacles that can be treated as specular reflectors. Thus, obstacles that are small relative to a wavelength, or distant from both the transmitter and the receiver (reader antenna and tag) have modest though nonnegligible effects, and tags may be read even though the straight-line path from reader to tag is obstructed.
Obstacles that are large compared to a wavelength, and close to either the reader antenna or the tag, are likely to prevent passive tags from being read. It is in this sense that RFID is a non-line-of-sight technology even for metallic obstacles.
That is, the total received power can change by (4.2+8.5) = 12.7 dB (a factor of 20) even though the reflected beams' combined power is only 20% of that of the direct beam. This sort of wild variation in received signal strength with small displacements in position or frequency is known as fading and is an ubiquitous problem in all radio systems. It is exacerbated in RFID because during the CW portion of an exchange, the reader transmits a very narrow spectrum with essentially only one frequency. Thus, nearly perfect cancellation is possible if directed and reflected beams happen to be of the right magnitudes and interfere destructively.
In United States operation, the reader will soon hop to a different frequency within the 902 to 928 MHz ISM band. The change in phase due to a hop from f1 to some other frequency f 2 is proportional to the difference in frequency and the difference in the length of the various paths.
For example, in Figure 3.35, the path length of the direct path might be (say) 1.5 m, and the path length to the wall and back to the tag would be 4.5 m; the path length difference is 3 m. Imagine that a tag is in a deep fade at some frequency f 1. If we shift the frequency by 10 MHz, the phase difference will change by 2π(10 MHz)(3 meters)/c = (6.28)(107)(3)/ (3 - 108) = 0.63 radian or about 36°.
This is more than enough to ensure that the signals no longer cancel at the new frequency, though the received power may still be below that of the direct beam on its own. However, in other jurisdictions much less bandwidth is available, and hopping may be impossible or ineffectual in defeating fades. For this reason, it is usually necessary to attempt multiple reads of a tag population in different physical configurations, for example, by moving the tags or rotating the objects to which they are attached, in order to ensure that all tags are read.
In RFID operation, the most important single reflector is the floor: RFID reader antennas, unlike many other communications systems, are typically oriented to transmit horizontally and are located within a meter or two of the floor. In many facilities, floors are constructed of concrete, which has a refractive index of around 2.5 at microwave frequencies, and can act as an effective reflector of incident radiation.
Since the concrete acts as a dielectric, the angle of incidence and the polarization of the incident beam are both of importance in determining the reflection coefficient. Vertically polarized radiation incident on a horizontal floor will experience no reflection at all at a particular angle of incidence, Brewster's angle, which is around 65° (measured with respect to the vertical) for microwave reflection from concrete (Figure 3.36).
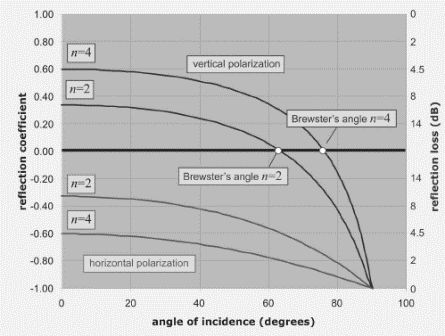
Horizontally polarized radiation benefits from no such effect; the reflection coefficient increases monotonically (and monotonously) with increasing angle from the normal. For a reader antenna placed 0.75 m above the floor, the Brewster's angle reflection point is about 1.5 m away, so the specularly reflected location is 3 m away, generally within the range of a typical UHF passive tag.
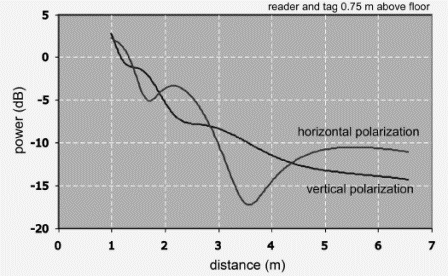
A vertically polarized antenna will experience no floor reflection at this distance, and thus produce little local fading (at least due to the floor reflection), whereas a horizontally polarized antenna will produce strong fading in this distance range (Figure 3.37). Thus, a reader using a linearly polarized antenna will produce more reproducible read results if the antenna is vertically polarized; on the other hand, a horizontally polarized antenna will display more prominent fades but also (sporadically) read more distant tags.
In the general case, with many irregular scatterers and reflectors present in uncontrolled positions and orientations, a propagation environment can be very complex and quite unpredictable. A simplified example is depicted in Figure 3.38 in which only reflection from walls and floor of a cubical room is incorporated. It is apparent that the signal strength varies in a complex fashion over size scales comparable to half-wavelength even for a fairly simple environment with no people or furniture. A tag moving within this environment will be easily read in certain regions, and very difficult to read when displaced in an arbitrary direction by 10 or 12 cm. In realistic environments, it is often necessary to attempt to read tags multiple times in differing physical configurations to ensure that all the tags are read.